# 第四章(上)-并行程序性能分析
渐入佳境
# 加速比 & 效率
加速比的定义为:
:最优串行算法的执行时间
:使用 p 个处理器的执行时间
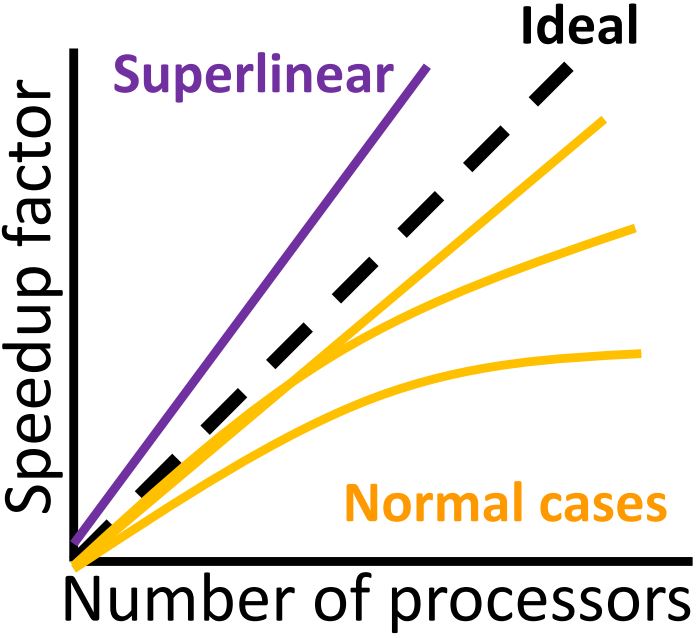
# 加速比
Linear speedup:
- 理论上理想的加速比
Superlinear speedup:
- 偶尔在实践中发生
- 额外的硬件资源(例如:memory)
- 软件或硬件的优化(例如:caching)
Maximum Speedup
- 达到理想的最大加速比 很困难
- 程序不是每个不都能并行化(导致处理器空闲)
- 在并行计算中需要额外的计算量(例如:同步的开销)
- 多个程序之间需要通信(通常是主要因素)
- 使 表示程序中无法并行的部分
- 假如处理器的数量趋向于无限大:
- 达到理想的最大加速比 很困难
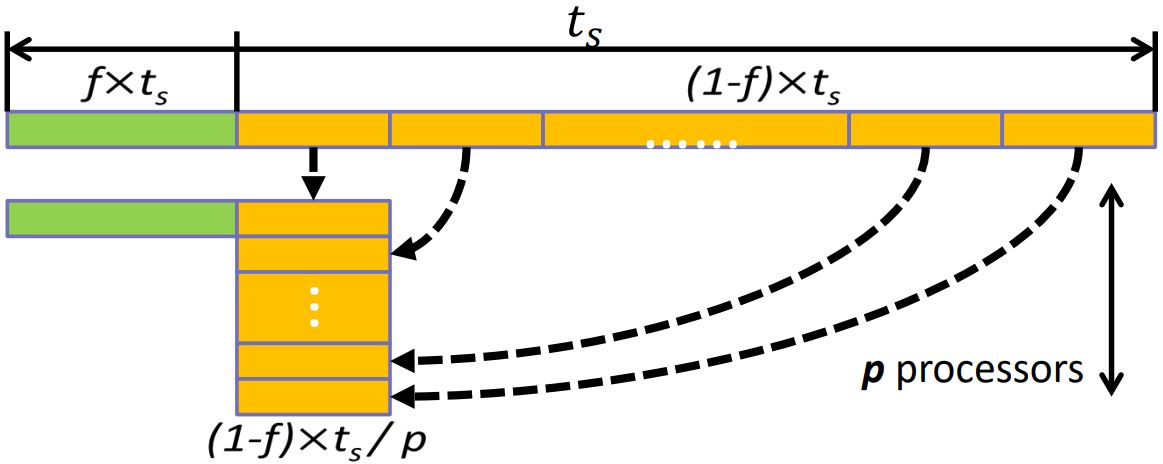
# 系统效率
System efficiency:
# 强扩展性 & 弱扩展性
# 强扩展性 strong scalability
- 针对一个问题,负载不变,处理器个数增加
- 旨在更快的解决一个问题
- 如果加速比等于处理器个数,就能实现线性规模的增加

# 弱扩展性 weak scalability
- 分配给每个处理器的负载保持固定,增加处理器的数量能够解决更大规模的问题
- 旨在用相同的时间解决更大规模的问题
- 运行时间不变,工作能够不断增加,可实现线性规模的增长
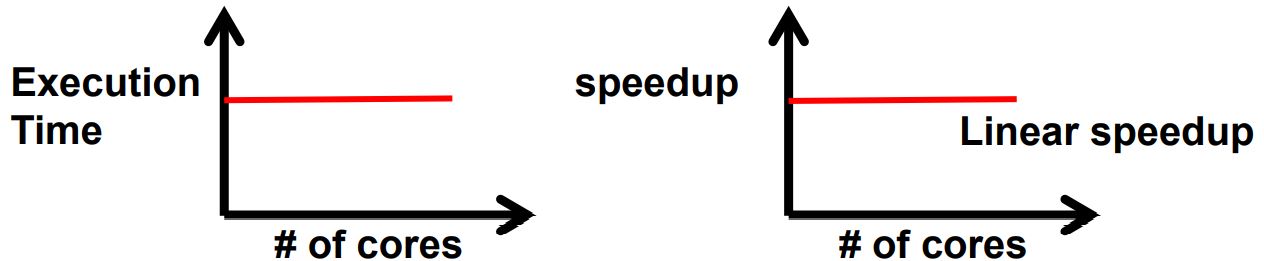
# 两者对比
| Strong scaling | Weak scaling |
|---|---|
| 线性规模难以实现,因为随着问题规模增加,通信开销也会同比例增加 | 线性规模增加容易实现,因为不管使用多少进程,通信开销相对固定 通信使用 nearest-neighbor communication patterns |
# 时间复杂度 & Cost optimality
本节的时间复杂度和代价优化不仅考虑了并行算法的设计,还考虑了并行部分的通信。
# Time Complexity Analysis
- : 并行算法的执行时间
- : 计算部分的消耗
- : 同步部分的消耗
- : 消息延迟(假设固定)
- : 一条数据的传输时间
- : 在一个消息中的数据的条数
- : 消息的数量
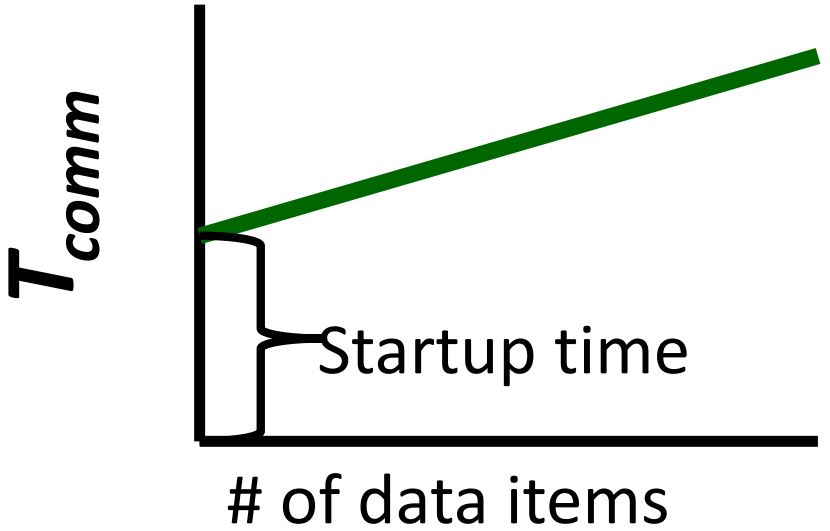
累加 个数字的并行算法设计:
★ 算法1
用2个计算机来并行计算:
- step-1. 电脑1把 个数发送给 电脑2
- step-2. 两台电脑同时加 个数
- step-3. 电脑2把部分和发送回电脑1
- step-4. 电脑1把两个部分和加起来得到最终结果
复杂度分析:
- Computation: (step-2 和 step-4)
- Communication: (step-1 和 step-3)
- 总体的时间复杂度:
★ 算法2
用m个处理器来并行计算:
(1)把 n 个数字平均的分给 m 个处理器
(2)m 个处理器同时相加 n/m 个数字
(3) 把 m 个部分和返回到一个处理器,相加得到最终结果
并行处理流程:
- Phase1: 把 n 个数字发送给 m 个 slaves
- Phase2: 累加部分和
- Phase3: 把结果发送给 master
- Phase4: 计算最终结果
- Overall: 时间复杂度
由上述两个算法例子可知:
◇ 处理器个数少,通信开销少,计算的时间复杂度更高
◇ 处理器个数多,通信开销大,计算的时间复杂度更少
所以设计并行算法需要在 computation 和 communication 之间做权衡。
# Cost Optimal Algorithm
- 定义
- 解决问题的代价随着在单个处理器上的执行时间成正比例关系
-
- : 执行串行算法的时间复杂度
- : 执行并行算法的时间复杂度
- 例子
- Sequential algorithm:
- Parallel algorithm 1: uses processor with
- Parallel algorithm 2: uses processor with
# 参考资料
Introduction parallel computing tutorial (opens new window)
台湾新竹清华大学 平行程式 (opens new window)
← 第三章-技术 第四章(下)-并行计算定理 →
